图 1 PCB微孔钻用硬质合金棒材的缺陷图：（a）裂纹缺陷；（b）未磨起缺陷；（c）磨面缺陷；（d）缺口缺陷
分享：硬质合金棒料上的两条裂纹有何影响
硬质合金由德国人施勒特尔发明于1923年，此后硬质合金工业便不断发展壮大。中国目前是世界上最大的硬质合金生产与消费国。从材料组成上说，硬质合金是由脆性的过渡族金属碳化物硬质相和韧性的铁族金属粘结相以及一些其他微量元素组成的复合材料[1]。就好比于钢筋混凝土通过结合钢筋与水泥，使其既耐压又抗拉。硬质合金中硬质相和粘结相的结合使其既具有高硬度、高强度，又有较好的韧性，因此广泛应用于刀具材料、钻探工具、测量工具和耐磨零件等[2−3]。在我国，切削工具的硬质合金用量约占整个硬质合金产量的1/3。近几年硬质合金在民用领域的应用也不断扩展，如表链、表壳、高级箱包的拉链头、硬质合金商标等。在制备过程中，硬质合金构件表面和内部常存在众多微小缺陷和局部损伤。以PCB微孔钻用硬质合金棒材为例，常见的表面和内部缺陷有：微裂纹、未磨起、磨面和缺口等，见图1。
疲劳与断裂是引起工程结构件失效的最主要的原因之一[4]。在钻孔、切削等循环载荷的作用下，这些缺陷和损伤逐步扩展并形成宏观裂纹，并会导致裂纹迅速扩展直至断裂失效[5]。为检验出厂的硬质合金棒料的品质是否合格，需对硬质合金棒料进行疲劳失效过程的仿真分析与实验研究。
疲劳失效过程可划分为裂纹萌生、裂纹扩展和断裂三个阶段。针对裂纹扩展阶段，目前主要有实验和数值计算两种方法[6]。由于实验研究的成本大、周期长，因此数值计算成为研究裂纹扩展的主要手段之一。许多学者对此进行了研究，并取得了相关成果[7−9]。刘建平[7]认为平齐、呈纤维状且无明显塑性变形的断口，为脆性断裂典型形貌。硬质合金棒料的断口同样有此形貌，故其为脆性断裂。于世光等[8]利用Franc3D基于边界元理论计算了半椭圆型表面三维表面裂纹前沿不同位置处的应力强度因子，结果表明裂纹最深处应力强度因子最大，与理论值具有很好的一致性。白树伟等[9]利用Abaqus有限元软件对CT试样的裂纹前缘进行数值模拟，发现在疲劳扩展中初始直裂纹将演变成椭圆形裂纹。鲁春鹏等[10]利用ANSYS有限元软件对环状V型缺口的圆柱件进行有限元分析，发现V型槽所在截面上的弯应力最大，分离断裂面会产生于V型槽处。Rao等[11]使用Franc3D和NASTRAN软件，进行了重型卡车车架裂纹的三维裂纹扩展，从而改进车架设计以防止微动疲劳。Triamlumlerd等[12]为研究加筋板尺寸和腹板间隙长度对疲劳裂纹扩展的影响，采用Franc3D软件进行应力强度因子、裂纹扩展和疲劳寿命分析。上述研究说明采用Abaqus、ANSYS和Franc3D等有限元软件对裂纹扩展过程的数值模拟具有很好的准确性，可以实现较为精确的裂纹扩展过程预测。硬质合金棒料危险截面附近微小裂纹会加剧疲劳和断裂的风险，有必要对此展开数值研究。
本文将在危险截面处带有双裂纹的硬质合金棒料作为上述疲劳扩展问题的研究模型，运用Franc3D和Abaqus软件进行仿真计算，研究当硬质合金棒料危险截面附近存在两条椭圆形裂纹时裂纹前沿的应力强度因子的变化趋势，模拟裂纹的扩展过程，并进而研究两条裂纹的相互影响，为硬质合金棒料在工程中应用的可靠性分析与优化提供理论基础和技术支撑。
1. 材料的裂纹扩展模拟
应力强度因子（SIF）是计算裂纹扩展速率和判断含裂纹材料断裂的重要参量。因此要进行裂纹扩展模拟，需要首先计算出裂纹前沿的应力强度因子并在此基础上完成裂纹扩展模拟。
1.1 应力强度因子
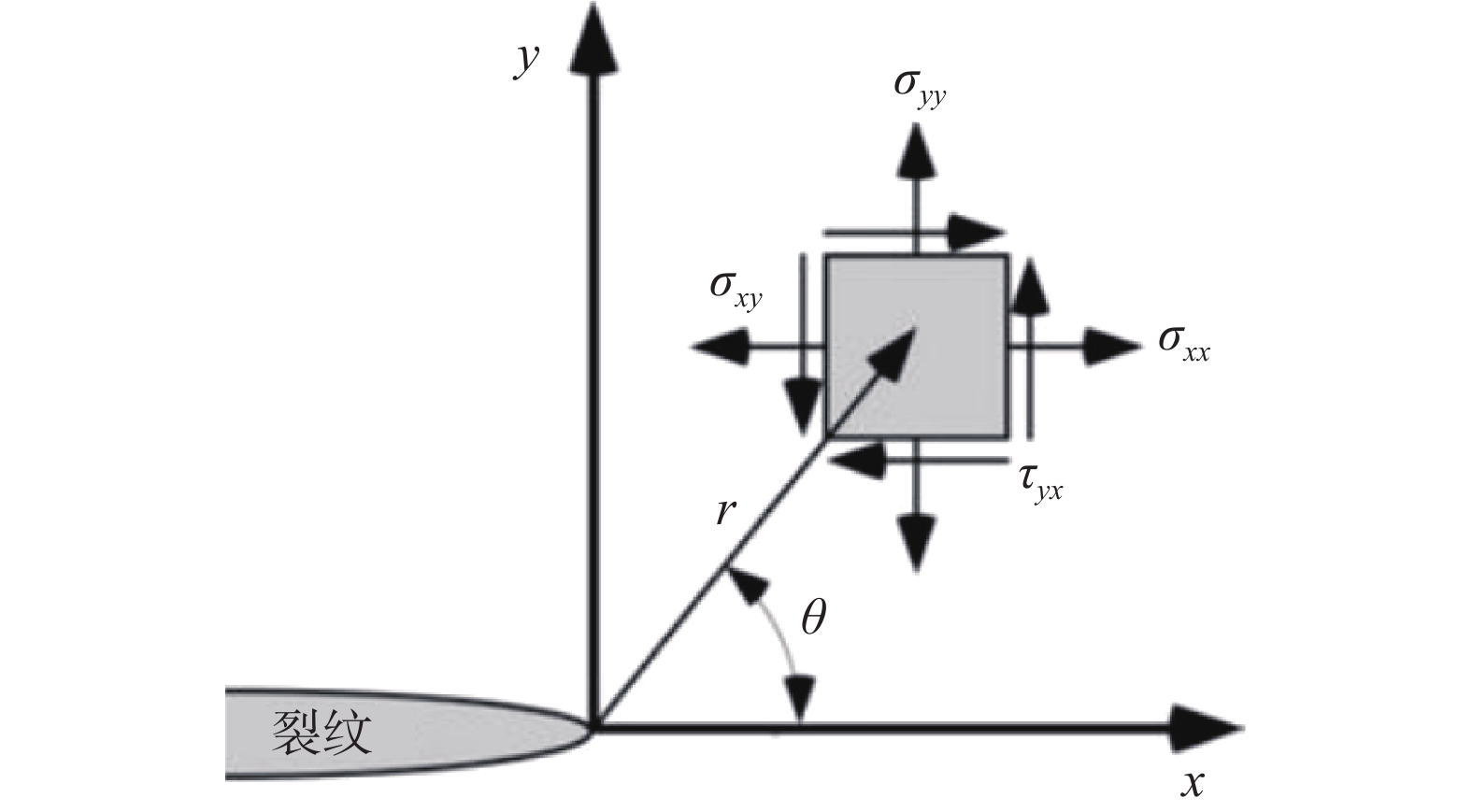
弹性体内部的裂纹前沿存在应力奇异现象，弹性断裂力学理论一般用应力强度因子（Stress intensity factor, SIF）来反映裂纹前沿弹性应力场的强弱。裂纹前沿应力场的分布与应力强度因子的函数关系与裂纹类型有关。裂纹的基本类型有三种，分别是Ⅰ型（张开型），Ⅱ型（滑移型）和Ⅲ型（撕开型）裂纹。Ⅰ型裂纹是工程中最常见的、危害最大的裂纹类型，也是硬质合金棒料中最常见的裂纹类型，本文将以Ⅰ型为例展开研究。
通过硬质合金棒材外观缺陷自动检测机的典型缺陷数据库，提取了以下两张Ⅰ型裂纹图片如图2：
Ⅰ型（张开型）裂纹在正应力的作用下，裂纹上下表面位移使裂纹张开，其裂纹尖端应力场如图3所示（τ为剪应力，σ为正应力）。应力强度因子K1定义为
|
|
(1) |
式中，r为裂纹尖端到微元的距离，
断裂力学研究表明，
|
|
(2) |
式中，
应力强度因子的理论计算方法可分为解析法和数值计算方法。常用解析法包括复变函数法、叠加法、权函数法，但仅适用于结构几何、载荷和裂纹形态等比较简单的情况，而数值计算方法则不受裂纹结构几何、载荷和裂纹复杂性的限制，因而得到广泛运用[13]。针对棒料裂纹扩展过程的数值计算通常借助于Abaqus和Franc3D软件。在Abaqus中建立完整模型，将局部模型和全局模型分别导入Franc3D，然后在局部模型中插入目标裂纹。应力强度因子计算前处理采用自适应网格划分方法，建模计算过程简单方便。
1.2 裂纹扩展模拟
在裂纹扩展阶段，常用Paris公式来描述裂纹扩展速率[14]。
|
|
(3) |
式中，
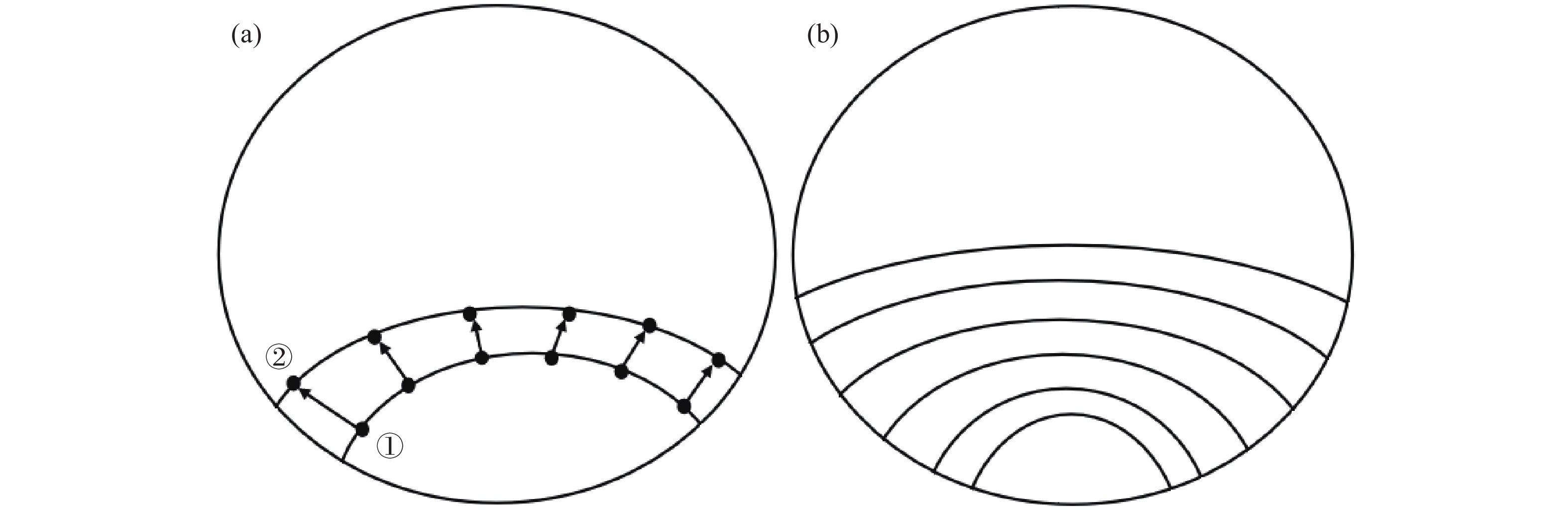
硬质合金棒料裂纹前沿在Franc3D中是由一系列节点组成的空间曲线，如图4（a）所示。对于裂纹①，在计算出每一节点的应力强度因子后，根据最大周向应力准则（裂纹沿最大周向应力的方向进行扩展）确定该节点的扩展方向，如图4（a）中箭头所示。各节点沿扩展方向扩展一定的裂纹增量后，得到下一个裂纹前沿，如图4（a）中裂纹②所示。其中，对于每个节点i的裂纹增量
|
|
(4) |
式中：
重复裂纹①到裂纹②的扩展过程，即可模拟整个裂纹扩展过程，如图4（b）所示。Franc3D采用自适应网格划分方法，只需要用户设置合理的裂纹增量
2. 建模与参数设置
2.1 材料参数
硬质合金具体参数如表1[15−16]所示，其中利用Paris公式表征棒料的裂纹扩展速率。
表 1 硬质合金仿真分析参数
| 杨氏模量/GPa | 泊松比 | 裂纹扩展参数，m | 裂纹扩展参数，C | 断裂韧性，KI/（MPa·m1/2） |
| 71.4 | 0.3 | 10.71 | 8.3112×10-19 | 11.12 |
| 注：断裂韧性KI是指应力强度因子K1增大到发生断裂时临界值 | ||||
2.2 几何尺寸与边界条件
将硬质合金棒料简化为悬臂梁模型，左侧为固定段，右侧为自由端，如图5（a）所示。参考现有硬质合金棒料产品的尺寸确定模型尺寸，棒料长0.30 m，直径0.02 m，在距离自由端长度为20 mm的半圆形面上施加沿半径方向的均布载荷P=3 MPa。以自由端圆心为原点建立直角坐标系，轴向为z轴，如图5（a）所示。固定端处弯矩最大，是危险截面，即材料力学中最大应力的截面。为研究裂纹间距的影响，将裂纹1固定在位置0，0.010和0.288 m处，选择4个不同位置，插入裂纹2。两道裂纹插入位置的局部放大示意图如图5（b）所示，两裂纹插入位置的坐标如表2所示，两个裂纹的裂纹面均垂直于轴线方向，初始裂纹半径为3×10−4 m。两裂纹中，裂纹1处的最大应力相对较小，裂纹2处的最大应力相对较大，研究裂纹位置范围内的最大应力曲线如图5（c）所示。
表 2 裂纹坐标及间距
| 编号 | 裂纹1的坐标/mm | 裂纹2的坐标/mm | 裂纹间距/mm |
| 1 | （0，10，288） | （0，10，292.0） | 4.0 |
| 2 | （0，10，288） | （0，10，293.0） | 5.0 |
| 3 | （0，10，288） | （0，10，293.5） | 5.5 |
| 4 | （0，10，288） | （0，10，294.0） | 6.0 |
3. 模拟结果与分析
采用Franc3D进行裂纹扩展模拟，设置循环载荷的应力比为R=0，即σmax/σmin=0。两条裂纹在裂纹扩展过程中的a–K1曲线如图6所示，其中一个数据点表示一次裂纹扩展；图片右上角的图注为：从图6可知，一般情况下，应力强度因子K1随着裂纹尺寸a的增大而增大。但在一种情况下例外，即在双裂纹互相影响且裂纹尺寸很小（a<1 mm）的情况下，裂纹1在扩展到一定程度之后会受到抑制，K1值下降。将裂纹1的应力强度因子K1首次下降时的两裂纹的裂纹尺寸、应力强度因子和裂纹扩展速率一并列出，如表3所示。由表3可得出以下结论：
表 3 裂纹1的K1值首次减小时两裂纹的相关参数
| 编号 | 裂纹2的z坐标/mm | 裂纹1尺寸，a/（10-4 m） | K1/（MPa·m1/2） | 裂纹扩展速率（da/dN）/（mm/次） | |||
| 裂纹1 | 裂纹2 | 裂纹1 | 裂纹2 | ||||
| 1 | 292.0 | 9.1 | 14.9 | 19.4 | 2.98 | 50.29 | |
| 2 | 293.0 | 3.9 | 12.1 | 19.3 | 0.32 | 47.58 | |
| 3 | 293.5 | 2.8 | 10.9 | 17.2 | 0.10 | 13.86 | |
| 4 | 294.0 | 2.6 | 10.7 | 17.9 | 0.09 | 21.24 | |
1. 随着两裂纹间距变大，应力较小处裂纹的应力强度因子K1首次下降时的裂纹尺寸a将减小。间距由4增加至6 mm，a减小为原来的29%。该现象意味着更早出现了抑制裂纹扩展的情况。
2. 应力较小处裂纹的应力强度因子K1首次减小时，应力较大处的裂纹尺寸、应力强度因子和扩展速率均远大于应力较小处，且随着载荷循环数的增加，两者各参数的差值将进一步增大。
综上所述，即便硬质合金棒料存在多个微小裂纹，也只需要分析应力较大截面上的裂纹扩展情况即可。
4. 结束语
本文针对硬质合金棒料表面双裂纹疲劳扩展问题，采用Franc3D软件，对硬质合金危险截面附近有两条裂纹的情况进行裂纹扩展模拟和分析，得到如下结论：裂纹尺寸仍然很小的情况下，硬质合金棒料上两条裂纹中的应力较小处的裂纹在扩展到一定程度之后会受到抑制，应力强度因子K1值下降；随着两条裂纹的间距变大，抑制裂纹扩展的情况将出现得更早。在本文的材料参数和工况情况下，间距由4增加至6 mm，应力较小处裂纹的应力强度因子K1首次下降时的裂纹尺寸a减小为原来的29%；从仿真计算结果来看，当硬质合金棒料存在多个微小裂纹时，应力较大截面上裂纹是造成断裂的主要原因。因此在简化分析中，可以只分析应力较大截面上裂纹的裂纹扩展情况。
文章来源——金属世界
浙公网安备 33042402000106号
