
分享:TC4 ELI钛合金高低周疲劳性能及寿命预测模型
0. 引言
钛合金轻质高强,具有优异的力学性能和耐腐蚀性能,在航空航天、汽车、医疗等领域得到广泛应用。关键钛制部件的服役环境较为复杂,频繁加卸载引起的疲劳载荷及装配公差引起的振动载荷是导致其失效的主要原因。因此,提升钛合金的疲劳性能、建立精准的寿命评估方法一直是该材料研究的焦点[1-3]。
金属材料的疲劳性能可分为低周疲劳和高周疲劳两个方面。低周疲劳通常在应变控制的低频大载荷作用下发生,其失效过程主要由裂纹萌生、扩展和最终断裂组成,具有明显的塑性变形特征[4];高周疲劳则是在相对较低的应力水平下循环加载后发生,其失效过程同样由裂纹萌生、扩展和断裂三部分组成[5]。在低周疲劳方面,研究主要集中在材料的塑性变形和裂纹行为方面,通过探究材料的微观结构、晶粒取向以及加载条件等因素,更好地理解低周疲劳失效机理[6];在高周疲劳方面,研究则更多地关注材料的表面和界面特性[7]。
低周疲劳和高周疲劳在实际工程中的失效机制和影响因素有所不同,同时预测低周和高周疲劳寿命的理论模型较为缺乏。在宏观尺度上,基于应力准则的寿命预测模型多用于预测高周疲劳寿命,如Basquin模型[8]、Morrow模型[9]和Goodman模型[10],而基于应变准则的寿命预测模型多用于预测低周疲劳寿命,如Manson-Coffin模型[11]。LI等[12]提出了一种基于能量密度的寿命预测模型,该模型在宏观尺度上可以精准预测镍基高温合金的低周和高周疲劳寿命,但需要大量试验数据进行参数拟合,并且该模型在钛合金疲劳寿命上的外推性有待解决。在微观尺度上,基于晶体塑性理论的疲劳指示因子(如累积塑性滑移[13]、应变能耗散[14]、应变统计学理论[15]和驻留滑移带能量[16])或疲劳寿命预测模型可以有效反映材料的微观演变特征[17]。王秀锐等[18]在累积塑性滑移的基础上考虑有效弹性应变发展了一种新的疲劳指示因子,对低周和高周疲劳寿命预测的准确性和稳定性都有所提高。但是,由于晶体塑性有限元模拟效率低且计算复杂,微观尺度的疲劳指示因子很难在工程上得到应用和推广。因此,构建一种计算简便且可以同时预测低周和高周疲劳寿命的模型成为关注重点。
作者对TC4 ELI钛合金进行室温低周和高周疲劳试验,研究了不同加载工况下的疲劳寿命分布和疲劳失效行为;基于有效应变能密度,建立一种可以同时预测钛合金低周和高周疲劳寿命的预测模型并进行了验证。
1. 试样制备与试验方法
试验材料为TC4 ELI钛合金,通过对10 kg铸锭进行2次真空自耗电弧熔炼,再进行多次锻造制备而成,锻坯尺寸为300 mm×60 mm×30 mm。对锻坯进行热处理,使原始锻态组织转变为细片层组织,在牺牲少部分强度的同时显著提高断裂韧性,以满足实际部件损伤容限设计需求。热处理制度基于钛合金相变行为和微观结构[19-20]确定,如下:在箱式电阻炉中将锻坯加热至955 ℃保温120 min固溶,使α相和β相均匀分布并消除加工过程中可能引入的内应力,随后升温至1 000 ℃保温40 min时效,以确保α相转变为β相并避免过长的保温时间导致β晶粒长大,空冷至室温;最后,在730 ℃下时效130 min以调控析出相,空冷。热处理后试验合金的显微组织如图1所示,为片层组织,与实际应用的关键构件材料组织[21]相同。
按照GB/T 228.1—2021《金属材料 拉伸试验 第1部分:室温试验方法》,在MTS 370型万能试验机上进行室温拉伸试验,先采用应变控制模式,应变速率为10−4 s−1,当总应变达到1%时,切换到位移控制模式,拉伸速度为0.01 mm·s−1,直至拉断为止。测得试验合金屈服强度与抗拉强度分别为817 MPa和910 MPa,断后伸长率为11.2%。
在试验合金上切取如图2所示的疲劳试样,进行打磨和抛光处理,按照GB/T 26077—2021《金属材料 疲劳试验 轴向应变控制方法》,采用Instron 8801型疲劳试验机在室温下进行低周疲劳试验,采用应变控制模式,载荷波形为三角波,应变速率为10−2 s−1,应变比为−1,应变幅分别为0.4%,0.6%,0.8%,在每个应变水平下各测4个有效数据点。按照GB/T 3075—2021《金属材料疲劳试验轴向力控制方法》,采用MTS 370型疲劳试验机在室温下进行高周疲劳试验,采用应力控制模式,载荷波形为正弦波,加载频率为10 Hz,应力比为0.1,最大应力分别为800,700,600 MPa,在每个应力水平下各测4个有效数据点。使用电火花线切割机从疲劳失效后的试样上切下断口(高度在3~5 mm),将断口置于乙醇中进行超声清洗,采用Apollo 300型扫描电子显微镜(SEM)观察疲劳断口形貌。
2. 试验结果与讨论
2.1 疲劳寿命分布
由图3可以看出:试验合金的疲劳寿命随着应变或应力水平的增加均显著缩短,当应变幅最小,为0.4%时疲劳寿命的分散性比较明显,而应力水平越高,疲劳寿命的分散程度越小。钛合金的显微组织特征会影响其在不同应变/应力水平下疲劳寿命的分散性:在较低应变或应力条件下,试验合金中的微观缺陷(如晶界、析出物、金属夹杂物等)会引起局部应力集中,进而加速裂纹萌生;而在高应变或高应力条件下,由于试验合金的塑性变形较大,疲劳裂纹的萌生和扩展更多依赖于材料的整体组织均匀性,微观缺陷对疲劳性能的影响较小,因此疲劳寿命分散性相对较低[22-24]。
2.2 疲劳断口形貌
由图4可以看出,试验合金的室温低周疲劳断口均由疲劳裂纹源区、疲劳裂纹扩展区和瞬断区3部分组成。裂纹源均出现在表面,在裂纹源区可以看到河流状散射条纹,条纹预示着裂纹扩展的方向;在裂纹扩展区可以观察到与裂纹扩展方向相垂直的多条相互平行的疲劳辉纹,每条辉纹代表着一次疲劳循环,疲劳辉纹的宽度随着应变幅降低而减小。
由图5可以看出,试验合金的高周疲劳断口均可划分为光滑的疲劳裂纹源区、呈河流状散射条纹的疲劳裂纹扩展区和粗糙的瞬断区。当最大应力为700,800 MPa时,疲劳裂纹均起源于表面,向内部扩展,形成疲劳裂纹扩展区,裂纹扩展区面积与瞬断区面积基本相同;当最大应力为600 MPa时,疲劳裂纹萌生于次表面,裂纹萌生后呈网状逐渐向内部和表面扩展,这说明在较低应力加载工况下,疲劳裂纹萌生对材料显微组织更加敏感。当最大应力从800 MPa减小到600 MPa时,试验合金的疲劳辉纹宽度从4.3 μm减小到1.6 μm,说明随着施加应力的增大,每一周次中裂纹扩展的距离增大。疲劳裂纹萌生位置除了与加载工况有关,还与材料的表面状态有关。一方面,材料表面容易存在微缺陷,如机械加工痕迹、凹坑、微裂纹等,这些表面缺陷在循环载荷作用下会引起应力集中,加速疲劳裂纹的萌生[25];另一方面,在疲劳加载过程中,材料表面承受的应力往往大于内部应力,此外表面的自由度更大,更容易产生局部塑性变形,从而为裂纹萌生提供有利条件。
3. 疲劳寿命预测
3.1 疲劳寿命预测模型的建立
对于低周疲劳加载工况,每次循环引起的疲劳损伤通常通过半寿命周次下的净拉伸滞后能来评估[26]。其中,由塑性变形引起的累积能量耗散被认为是确定疲劳损伤的一个重要参量,其表达式为
| (1) |
式中:dold,f为每个周次下的疲劳损伤;af,bf均为损伤模型参数;Δεp为半寿命周次下的塑性应变范围;σmax为最大应力。
然而,这种疲劳损伤模型很难用于计算高周疲劳损伤值,主要原因是高周疲劳条件下试样承受的最大载荷总是低于材料的屈服强度,不发生明显的塑性变形。尽管高周疲劳时材料在宏观尺度上呈现完全弹性变形,但是由于晶粒间的取向差不同,材料在微观尺度上仍然会发生局部塑性累积。基于此,研究人员基于晶体塑性理论建立了疲劳寿命预测模型,用于同时预测低周和高周疲劳寿命[13,18]。然而,这类微观模型计算复杂且效率低,很难在工程应用中得到推广。基于有效能量密度,作者建立了一种用于同时预测材料低周和高周疲劳寿命的宏观疲劳损伤模型,其概念如图6所示,图中:wel为弹性有效能量密度;wpl为塑性有效能量密度;σlimit为疲劳极限;Δσ为疲劳极限以上的应力水平;weff为有效能量密度。材料的疲劳极限根据传统的S-N曲线确定,疲劳极限以上的应力被定义为在低周和高周疲劳载荷下能引起疲劳损伤的有效应力[27]。有效能量密度包含弹性有效能量密度和塑性有效能量密度,其值由图6中阴影区域面积获得,计算公式为
| (2) |
式中:Δεe为半寿命周次下的弹性应变范围。
疲劳循环次数和有效能量密度之间的关系可以描述为
| (3) |
式中:Nf为疲劳循环次数;mf,nf均为材料常数。
新的疲劳损伤模型可以写成
|
|
(4) |
式中:df为每周次循环引起的疲劳损伤。
疲劳损伤模型参数需要通过对疲劳试验数据进行拟合获得。对疲劳寿命和有效能量密度进行拟合,拟合结果见图7,得到模型参数mf为2.866×106周次,nf为1.49。
3.2 疲劳寿命预测结果与分析
假设当疲劳损伤累积到1时,材料发生失效。由图8可以看出,建立的疲劳损伤模型展示了准确的预测能力,有92%的高周和低周疲劳寿命数据落在±3.0误差带范围内。
4. 结论
(1)在室温、不同应变幅条件下,低周疲劳裂纹均在TC4 ELI钛合金表面萌生;在室温、较低最大应力(600 MPa)条件下,高周疲劳裂纹倾向于萌生在合金次表面,在较高最大应力(700,800 MPa)条件下,高周疲劳裂纹倾向于在合金表面萌生。
(2)92%的低周和高周疲劳预测寿命数据落在±3.0误差带范围内,说明基于有效能量密度构建的疲劳寿命预测模型能够较准确地同时预测TC4 ELI钛合金的低周和高周疲劳寿命。
文章来源——材料与测试网










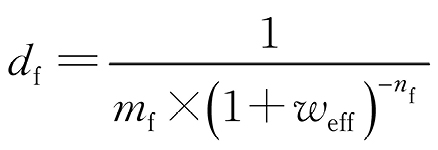



 浙公网安备 33042402000106号
浙公网安备 33042402000106号

