
分享:耐磨钢高温压缩变形的本构模型构建及热加工图
0. 引言
钢铁材料如今正向着更高强、更耐磨的方向发展,同时为了追求绿色发展,耐磨钢产品需求呈现爆发性增长。在热连轧高强钢产品的研发方面,鞍钢放弃了传统合金化耐磨钢的生产模式,提出使用控轧控冷(TMCP)工艺,应用相变强化的机理实现超高强耐磨钢产品的生产[1],即以低合金碳素钢为基础,提高硅和铝的含量,借助TMCP工艺精准控制各相体积分数,冷却后得到铁素体+马氏体+残余奥氏体的多相组织,以实现耐磨钢的高抗拉低屈强比的综合性能。所生产的耐磨钢在成形性、耐磨性能、焊接性等方面都表现良好,被广泛应用到搅拌罐壳体及叶片等相关部件[2]。
为了确定具体的热连轧工艺,减少实际生产调试带来的资源浪费,需要借助数值模拟对材料在不同工艺下的变形行为进行预测,而数值模拟的基础是基于材料的热变形行为建立材料的本构模型[3]。目前,学者们已经对不同工艺(变形温度、应变速率等)下材料的热变形行为以及本构模型进行了研究[4]。耐磨钢主要采用热连轧工艺生产而成,温度在800~1 200 ℃,应变速率为约10 s−1中等水平,但是未见在该工艺参数范围内适用于耐磨钢的本构模型[5]。作者以鞍钢2150ASP生产线生产的耐磨钢为研究对象,利用单道次热压缩试验研究了该钢在高温中等水平应变速率下的流变行为;根据热变形过程中的真应力-真应变数据,引入真应变的影响对传统Arrhenius方程进行改进后建立本构模型,并绘制热加工图,确定合理的加工区间,以期为耐磨钢热连轧工艺的制定提供理论指导。
1. 试样制备与试验方法
试验材料取自鞍钢2150ASP热连轧生产线生产的耐磨钢中间坯,其化学成分(质量分数/%)为≤0.15 C,≤1.2 Si,≤1.75 Mn,≤0.015 P,≤0.005 S,≤0.022 Ti,≤0.45 Al,余Fe。在耐磨钢板坯中部区域取样,并沿厚度方向加工成尺寸为?8 mm×15 mm的圆柱体试样。
在Gleeble-3800型热模拟试验机上进行单道次热压缩试验,试验环境为真空环境。先以10 ℃·s−1的升温速率将试样加热至1 220 ℃,保温5 min,再以5 ℃·s−1的速率降温至变形温度(1 200,1 100,1 000,900,800 ℃)并保温15 s后,采用不同应变速率(0.1,1,5,10 s−1)进行压缩变形,变形量为70%。
2. 结果与讨论
2.1 热压缩变形行为
由图1可以看出,试验钢的流变应力随着变形温度的升高而降低,随着应变速率的增加而升高。随着变形量的增加,晶界间位错密度的堆积导致加工硬化,宏观表现为真应力增大;当真应力达到峰值应力后,动态再结晶的软化作用与加工硬化达到平衡状态,当二者持续保持平衡,则宏观表现为随着变形量的增加,真应力几乎保持不变。但是,在高温(不低于1 100 ℃)和低应变速率(0.1 s−1)条件下,试验钢的动态再结晶软化作用更强,因此随着变形量的增加,真应力达到峰值应力后出现略微降低的现象,随后当软化作用与加工硬化作用平衡后趋于稳定[6]。
2.2 本构模型的建立
为准确表征试验钢的真应力、真应变关系,对传统Arrhenius方程[7]进行改进,即在方程中引入真应变的影响。传统Arrhenius方程如下:
|
|
(1) |
式中:
在真应变ε为0.1条件下对式(1)两侧同时取自然对数,对不同变形温度下的ln
Zener-Hollomon提出了用变形温度和应变速率来表述高温变形条件对材料组织影响的数学模型,并定义Z参数为变形速率与温度的补偿因子[8],结合Arrhenius方程得到:
| (2) |
将式(2)两侧取自然对数后,对ln Z-ln[sinh(ασ)]进行线性拟合,结果如图4所示。通过求取纵轴截距得到ln A=24.93,进而得到A=2.576×1022。
由此得到真应力为0.1条件下的本构方程:
|
|
(3) |
同理,参照上述推演过程对真应变为0.2~0.9条件下的模型参数进行求解,结果如表1所示。利用四次多项式对不同模型参数与真应变的关系进行拟合,拟合结果如图5所示,拟合公式如下:
|
|
(4) |
| 真应变 | α | n | Q/(J·mol−1) | A |
|---|---|---|---|---|
| 0.1 | 0.008 1 | 8.33 | 328 363.4 | 2.58×1022 |
| 0.2 | 0.007 5 | 6.56 | 297 935.7 | 2.35×1017 |
| 0.3 | 0.007 0 | 6.38 | 297 075.0 | 1.82×1017 |
| 0.4 | 0.006 9 | 6.28 | 299 123.2 | 2.90×1017 |
| 0.5 | 0.006 8 | 6.15 | 298 841.8 | 3.36×1017 |
| 0.6 | 0.006 7 | 6.00 | 297 640.3 | 2.84×1017 |
| 0.7 | 0.006 5 | 6.08 | 302 700.1 | 8.91×1017 |
| 0.8 | 0.006 3 | 6.45 | 318 719.0 | 2.00×1019 |
| 0.9 | 0.006 1 | 7.20 | 349 336.2 | 8.54×1021 |
结合式(1)与式(4)即可得到试验钢的本构模型,从而预测其流变行为。将模型预测结果与试验结果进行对比,由图6可以看出,模型预测结果与试验结果吻合较好,真应力的平均相对误差为3.79%。为了使预测结果和试验结果的对比更直观,将真应力预测值与试验值进行线性拟合,结果如图7所示,计算得到线性相关系数R为0.997 5。线性相关系数越靠近1,说明二者的正线性相关性越强[9]。可知,预测值与试验值具有明显的线性正相关。综上,所建立的本构模型能够准确预测耐磨钢的高温流变行为。
2.3 热加工图的绘制
材料的热加工性能是指在塑性变形过程中材料不发生失稳破坏所能达到的变形能力。为了描述金属的热变形,常采用材料动态数学模型进行表征,并通过建立热加工图反映金属材料在不同条件下的热加工性能和稳定性[10]。基于材料动态理论,在热加工过程中,外界载荷的能量存在2种释放路径:一部分促使材料发生变形,另一部分促使材料发生组织演变[11]。具体的数学表达式如下:
| (5) |
式中:P为变形时的外界载荷;G为材料发生塑性变形时所需的能量;J为材料发生显微组织演变所需的能量。
2种能量释放方式均与应力和应变速率有关,因此提出了应变速率敏感系数[12],用来描述应力和应变速率之间的数学关系:
| (6) |
式中:K为材料变形常数;m为应变速率敏感系数。
式(6)两边取自然对数及偏导数,可得到应变速率敏感指数表达式:
| (7) |
功率耗散因子定义为耗散协量和材料理想线性耗散协量的比值,理想耗散状态是当m=1时的状态,因此功率耗散因子的表达式为
| (8) |
式中:η为功率耗散因子;J为耗散协量,J;Jmax为理想线性耗散协量,J。
基于应变速率和变形温度对应的功率耗散因子建立等高线图,即功率耗散图。材料的变形并非是无止境的,高的功率耗散因子说明材料组织演变剧烈,但是若要对材料的加工性能进行评定,则需引入失稳判据ξ[13]:
| (9) |
当ξ≤0时,材料会发生变形失稳。基于失稳判据建立等高线图,即可得到材料的失稳区间图。将材料的功率耗散图和失稳区间图进行叠加,即得到材料的热加工图;根据变形量的大小将多个热加工图叠加则可得到材料的多维度热加工图。当真应变为0.3,0.5,0.7,0.9时,试验钢的三维热加工图如图8所示,图中灰色区域为失稳区。由图8可以看出,当真应变为0.3时,材料处于小变形应力状态,几乎不发生失稳。在低温低应变速率条件下功率耗散不明显,在高温低应变速率的条件下,功率耗散较明显,这是因为温度升高降低了材料再结晶的驱动力,使得材料易发生再结晶;在高温高应变速率条件下,材料不容易发生再结晶,但容易发生变形失稳。结合应力-应变曲线分析可知,在小变形时载荷释放的主要路径是变形而非显微组织演变[14]。当真应变为0.5时,材料处于中等变形的应力状态,失稳区开始增多,但此时材料并未发生明显的变形失稳。当真应变大于0.5时,材料处于大变形应力状态,失稳区更加明显,说明该条件下不适合进行单道次压缩变形,应采取多道次组合来施加载荷。综上可推断出,在单道次压缩变形时,试验钢合理的变形区间为真应变不大于0.5、应变速率不大于10 s−1、变形温度900~1 100 ℃。
3. 结论
(1)试验钢的流变应力随着变形温度的升高而降低,随着应变速率的增加而升高;随着变形量的增加,真应力先增加至峰值应力后趋于稳定,但在高温(不低于1 100 ℃)和低应变速率(0.1 s−1)下真应力达到峰值应力后先略微降低后趋于稳定。
(2)通过引入真应变的影响对传统Arrhenius方程进行改进而建立的本构模型可对试验钢在800~1 200 ℃变形温度和0.1~10 s−1应变速率下的高温流变行为进行预测,真应力预测值与试验值的平均相对误差约为3.79%。
(3)试验钢在单道次热压缩变形时的合理加工区间为真应变不大于0.5、应变速率不大于10 s−1、变形温度900~1 100 ℃。
文章来源——材料与测试网





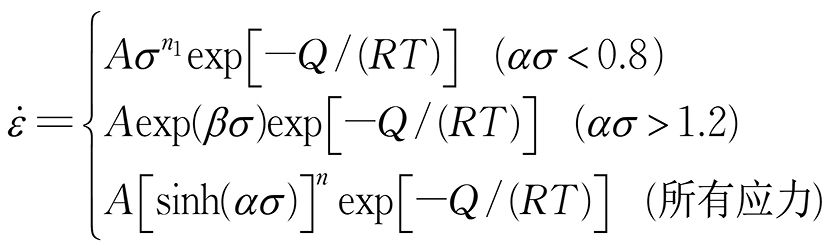



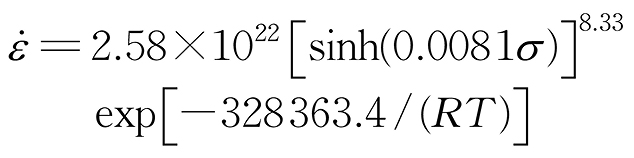
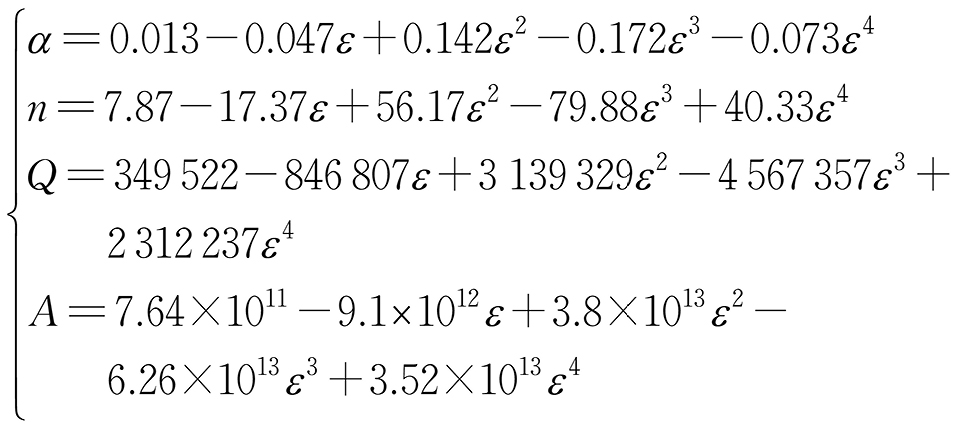





 浙公网安备 33042402000106号
浙公网安备 33042402000106号

