
分享:基于粒子群优化后随机森林模型的管道内腐蚀风险预测
随着国家经济的高速发展,对油气资源的需求越来越大,油气田开采力度不断扩大,油气井数量不断增加,集输管道里程持续增加,管道内部输送介质的腐蚀性加剧,使得与此相关的管道腐蚀问题越来越严重。腐蚀带来的管道爆裂、原油泄漏等问题严重影响了国家和企业的发展。原油和天然气为易燃、易爆物质,有时还含有硫化氢等有毒气体,石油与天然气管道始终是能源行业安全监管的重点领域之一。油气集输管道输送工艺和介质复杂、内腐蚀影响因素众多,腐蚀发生发展机制类型多样,例如塔河油田管道所处工况环境复杂,具有“五高一低”特点(高H2O、高CO2、高H2S、高Cl-、高矿化度、低pH),极易造成管道腐蚀与穿孔[1]。在管道轴向里程位置、管道环向时钟位置上,腐蚀的发生各具特点,多数情况下局部腐蚀的出现由多个因素或机制协同作用引起,这使得内腐蚀风险预测更为困难。
近年来,随着机器学习、人工智能等大数据技术的发展,机器学习技术逐渐进入工业领域,并在油气管道缺陷智能识别[2]、管道漏磁内检测、管道剩余寿命预测[3]等方面发挥着重要作用。MICHAEL等[4]基于油气田集输管道在线内检测数据训练贝叶斯网络,使用训练好的模型对没有在线检测数据的管道进行预测,结果表明,该贝叶斯网络模型可以对管道的内部腐蚀进行准确的预测。凌晓等[5]充分利用某输油管道检测数据集,针对反向传播神经网络(BPNN)模型的起始权值和阈值的优化问题,采用遗传算法(GA)进行参数寻优,有效克服了单一BPNN模型易陷入局部极值的问题,大幅提升预测精度,为管道完整性管理提供可靠的理论依据和决策支持。
作者以塔河油田历史失效数据为基础,利用皮尔逊(Pearson)相关系数和灰色关联度分析的方法明确管道内腐蚀主控因素,通过粒子群(PSO)算法对随机森林(RF)算法进行超参数优化,基于优化后的算法建立塔河油田管道内腐蚀风险预测模型,为油气田管道的腐蚀预警与防护提供帮助。
1. 管道内腐蚀影响因素
油气集输管道腐蚀的影响因素主要包括温度、CO2/H2S含量、水化学、流速、钢的成分和表面状态等,钢表面腐蚀产物性质会随着影响因素的变化而改变,从而对腐蚀速率产生显著影响[6]。
1.1 H2S、CO2含量的影响
当H2S和CO2同时存在时,H2S腐蚀和CO2腐蚀之间存在协同和竞争关系,腐蚀过程比较复杂[7]。SKILBRED等[8]认为,当系统中同时存在H2S和CO2时,可以根据其分压比p(CO2)/p(H2S)大致判断腐蚀主导因素是H2S还是CO2。当腐蚀过程以H2S的腐蚀反应为主时,主要产生各种类型的铁硫化物;当腐蚀反应由CO2腐蚀反应控制时,主要产生FeCO3;当腐蚀反应是两种气体腐蚀共同控制时,会同时生成各种铁硫化物和FeCO3。
1.2 温度的影响
温度对腐蚀的影响主要通过影响腐蚀产物的形成来实现。在不同环境条件下,随着温度升高,钢表面生成的腐蚀产物膜可能对腐蚀有促进作用,也可能有抑制作用。ABD等[9]使用HYSYS软件模拟了湿气管道的CO2腐蚀。当温度低于40 ℃时,由于碳酸铁层的高溶解度,管道表面没有形成保护膜,腐蚀速率随温度的升高而增大;当温度超过40 ℃时,管壁上形成致密的腐蚀产物膜,对基体起到保护作用,腐蚀速率降低。
1.3 pH的影响
SUN等[10]研究发现,pH可以通过影响电化学机制和表面保护性FeCO3膜的形成来影响碳钢的CO2腐蚀。在多相流工况下,当pH高于6.2时,钢表面能够形成保护性的腐蚀产物膜,因此pH升高能够明显降低腐蚀速率。MORAES等[11]的研究表明,pH升高会抑制H+的阴极反应,使Fe的阳极溶解减缓,因此腐蚀速率降低。此外,钢表面形成的碳酸盐腐蚀产物膜能够对钢基体起到保护作用,而溶液pH升高会抑制碳酸盐的溶解,进而降低腐蚀速率。
2. 基本原理
2.1 粒子群算法
作者采用粒子群优化算法对随机森林模型的超参数进行优化,该算法受鸟类捕食行为的启发,依靠群体智能随机搜索,通过粒子之间相互合作共享位置和适应度信息逐渐收敛到全局最优解[12]。如果将参数的最优解假设为其值域空间中一个兼具位置和速度属性的粒子,且寻优过程中的最优解由适应值(Fitness value)决定[13],具体迭代公式如下:
|
|
(1) |
|
|
(2) |
式中: 和
和 分别为粒子i在第j次迭代过程中第n维的速度和位置;
分别为粒子i在第j次迭代过程中第n维的速度和位置; 是粒子i在第n维中自身最优解的位置,
是粒子i在第n维中自身最优解的位置, 是群体在第n维中全局最优解的位置,每个粒子通过不断追踪这两个最优解进行更新;c1和c2为学习因子;rand(0,1)为由计算过程随机生成的(0,1)区间的随机数;w为惯性权重。
是群体在第n维中全局最优解的位置,每个粒子通过不断追踪这两个最优解进行更新;c1和c2为学习因子;rand(0,1)为由计算过程随机生成的(0,1)区间的随机数;w为惯性权重。
2.2 随机森林算法
随机森林算法是一种高效且用户友好的集成机器学习技术,可用于开发预测模型,通常用于回归、分类以及特征选择问题。随机森林的概念最早在1995年由HO[14]提出,随后BREIMAN[15]在2001年提出随机森林算法并对该算法进行了系统阐述。随机森林模型在回归问题上应用广泛,可有效解决传统机器学习模型在训练和预测过程中容易出现的过拟合问题,与其他机器学习模型相比,其训练速度更快、鲁棒性更强、预测效果更好[16]。图1为随机森林算法的模型。
3. 建模流程
基于PSO-RF算法的管道内腐蚀风险预测模型(以下简称PSO-RF模型)的建模流程如图2所示。建模主要步骤包括:确定模型的输入输出变量;划分数据集为训练集和测试集;模型参数的优选和优化;模型训练和评估。
3.1 确定模型的输入输出变量
在建立的PSO-RF模型中,选择管道腐蚀速率作为模型输出变量,管道腐蚀影响因素作为输入变量。值得注意的是,样本数据在使用之前需经过归一化处理,以消除管道腐蚀因素数据集单位和维度的影响,提高获得最优解的速度,防止数据爆炸[17]。另外,考虑到某些特征如腐蚀影响因素与腐蚀速率的相关性较弱,即对腐蚀速率的贡献率较小,这些弱相关特征的存在会对模型的训练产生一定的干扰,导致模型泛化能力差,预测精度变低。故利用Pearson相关性分析和灰色关联度分析来确定影响腐蚀速率的主控因素,进而确定模型的输入变量。
3.2 划分数据集为训练集和测试集
数据集的划分对模型的训练和测试至关重要。在训练模型之前,首先使用sklearn库中的数据集划分函数train_test_split()对数据样本进行随机划分,训练集和测试集样本分别占总样本数的80%和20%,其中训练集用于训练和构建模型,测试集用于模型的预测和评估检验。
3.3 模型参数的优选和优化
对于随机森林算法而言,其超参数的选择将直接影响模型预测的准确性,而一般的网格搜索方法有一定的局限性,寻优次数较多且容易陷入局部最优解。为了尽可能缩小预测误差,找到全局最优解,作者选择粒子群算法对参数进行优选和优化,然后再使用随机森林算法对相关数据进行训练和预测。
3.4 模型训练和评估
最后使用训练集对PSO-RF模型进行训练,并使用测试数据集来评估模型的准确性。作者选择决定系数(R2)、平均绝对误差(σMAE)和均方根误差(σRMSE)来评估模型的预测精度[18],计算公式分别见式(3)~(5)。决定系数R2的值介于0~1,其值越接近于1,表示模型的拟合度越好,模型预测结果越准确[19]。
|
|
(3) |
|
|
(4) |
|
|
(5) |
式中:n表示样本总量;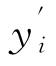 和yi分别表示测试样本的预测值和实际值。
和yi分别表示测试样本的预测值和实际值。
4. 实例应用
4.1 建立数据集
作者以Python编程语言为基础,使用Spyder.8软件进行编程。从塔河油田历年失效分析报告中的失效数据中共收集了603组数据作为预测模型的数据集。预测模型的输入变量为影响管道腐蚀的因素,包括以下六个方面:总压力、温度、H2S分压、CO2分压、Cl-含量和含水率。输出变量为管道在服役期间的平均腐蚀速率,利用首次穿孔刺漏时间、管线投产时间以及管线壁厚计算得到。表1为所有数据的范围及统计特性,使用最大值、最小值和平均值来描述。
| 特征数据 | 总压力/MPa | 温度/℃ | H2S分压/MPa | CO2分压/MPa | Cl-质量浓度/(g·L-1) | 含水率/% | 腐蚀速率/(mm·a-1) |
|---|---|---|---|---|---|---|---|
| 最大值 | 70.00 | 89.0 | 2.00 | 0.18 | 170 | 100.00 | 8.33 |
| 最小值 | 0.10 | 6.0 | 0.00 | 0.00 | 90 | 0.10 | 0.19 |
| 平均值 | 1.28 | 48.7 | 0.01 | 0.08 | 127 | 41.26 | 0.98 |
4.2 确定管道腐蚀主控因素
利用Pearson相关性分析以及灰色关联度分析方法对油田管道腐蚀的主控因素进行研究,对输入数据进行数据降维,提高模型的准确性。其中,Pearson相关系数(r)广泛用于评估两个变量之间的相关程度,其定义为协方差和标准差的商,它的值介于-1~+1。正值表示正线性相关,负值表示负线性相关。该值越接近+1或-1,线性相关性越强。而灰色关联度分析是根据各因素之间相似或者相异的发展趋势,也就是“灰色关联度”来衡量各因素或系统之间的关联程度[20]。
塔河油田输油管道腐蚀因素与腐蚀速率的Pearson相关性分析结果如图3所示。图中用蓝色表示正相关,红色表示负相关,颜色的深浅表示相关性的强弱(完全不相关时为白色,完全相关时为深蓝或深红)。从图3中可以看出,CO2分压、温度、Cl-含量和H2S分压与腐蚀速率的相关性为强相关;含水率和压力与腐蚀速率的相关性为弱相关。
塔河油田输油管道腐蚀因素与腐蚀速率的灰色关联度分析结果如图4所示。从图4中可以看出,管道内腐蚀速率与温度、压力、H2S分压、CO2分压、Cl-含量和含水率等影响因素的灰色关联度从大到小排序为:CO2分压(0.29)、温度(0.233)、Cl-含量(0.218)、H2S分压(0.211)、含水率(0.031)、压力(0.017)。
综合以上分析结果,确定CO2分压、温度、Cl-含量和H2S分压这4个因素作为塔河油田管道内腐蚀因素的主控因素。
4.3 模型参数设置
超参数的选择将直接影响模型预测的准确性,为提高随机随机森林模型的预测精度,使用粒子群优化算法寻求模型参数的最优值,在参数寻优过程中,使用R2作为粒子群优化算法的适应度值。RODRIGUEZ-GALIANO等[21]通过优化随机森林中决策树的个数(n_estimators)和构建最优决策树模型时考虑的最大特征数(max_features)来提高模型的准确性;除此之外,还有一些学者将决策树最大深度(max_depth)[22]作为优化参数。本文中使用粒子群优化的随机森林超参数包括:n_estimators、max_features和max_depth。设置参数的搜索区间如下:n_estimators∈[10,5000],max_features∈[0,5],max_depth∈[10,1000]。粒子群规模N=10,最大迭代次数K=200,惯性权重因子w=0.4,学习因子c1=c2=2。通过2 000次寻优最终确定随机森林模型的最佳参数组合为[n_estimators:1656,max_features:,max_depth:96]。
4.4 模型结果与分析
将Pearson相关性分析和灰色关联度分析后得到的4个腐蚀主控因素CO2分压、温度、Cl-含量和H2S分压作为随机森林模型的输入参数,结合前面所得的参数最优值,通过训练集数据训练并建立塔河油田金属管道腐蚀风险预测模型,使用测试集数据对模型的精度和可靠性进行评估。
首先为验证使用Pearson相关性分析和灰色关联度分析进行腐蚀主控因素选择即特征降维的有效性,将特征降维前后PSO-RF模型的预测结果进行对比,如图5所示。从图5中可以看出,在特征降维之前即模型输入特征为所有腐蚀因素时,模型预测的腐蚀速率与实际腐蚀速率差别较大,R2为0.81,模型预测精度较低。这是因为输入特征中存在弱相关因素,其对模型的预测造成了干扰,导致模型预测精度变低。特征降维后,仅以腐蚀主控因素作为模型的输入特征,此时模型的R2提升至0.97,预测精度有了大幅提升,模型预测的腐蚀速率更接近于实际值,预测误差大大降低。这表明Pearson相关性分析和灰色关联度分析相结合得到的腐蚀主控因素包含了影响腐蚀的主要信息,且该方法从腐蚀影响因素中去除了冗余信息,有效提高了模型预测精度。
在复杂的机器学习模型训练的过程中,经常会出现过拟合现象,从而导致模型泛化能力差。为验证该PSO-RF模型是否存在过拟合问题,将训练集和测试集数据输入该模型进行预测,结果如图6所示。表2列出了该模型在训练集和测试集上的预测误差及拟合情况。可以发现,PSO-RF模型在训练和测试过程中都有较好的拟合效果,R2分别为0.99和0.97,且训练集和预测集误差相差不大,表明该模型在对未知数据的预测过程中也有很好的表现,没有出现过拟合现象。
| 数据集 | σMAE | σRMSE | R2 |
|---|---|---|---|
| 训练集 | 0.008 | 0.07 | 0.99 |
| 测试集 | 0.027 | 0.161 | 0.97 |
为验证PSO-RF模型的预测效果,另外设置三个对比模型:BP神经网络(BPNN)模型、网格搜索优化的随机森林(GS-RF)模型以及遗传算法优化的随机森林(GA-RF)模型。所有模型的输入特征均为降维后的特征,模型预测对比结果如图7所示。
由图7可知,BPNN模型的预测效果最差,R2仅为0.83,腐蚀速率预测值与实际值差别较大,误差最大,σRMSE和σMAE分别达到0.381和0.179。其原因在于BPNN模型易陷入局部最小值,从而影响模型的预测精度。相对于BPNN模型,GS-RF模型和GA-RF模型的预测效果有了显著的提升,R2分别达到0.87和0.92,其预测误差也明显减小,σRMSE分别降为0.337和0.251,σMAE分别降为0.127和0.063,预测精度明显提升。其中GA-RF模型的寻优次数远少于GS-RF模型,且能够发挥遗传算法的全局寻优能力。PSO-RF模型的预测结果最优,R2达到0.97,且误差最小,σRMSE和σMAE分别为0.161和0.027,模型的预测准确度大大提升,相比于GA-RF模型,PSO-RF模型除了具有全局寻优能力,同时拥有高效的信息共享机制,因此能够快速收敛至全局最优值,使随机森林模型获得最优超参数组合。
4种模型的腐蚀速率预测值与实际值的相关性分析分别如图8所示。结果表明,在这4种模型中,PSO-RF模型的预测值与实际值最接近,除个别数据点之外,其余数据点基本可以拟合为一条直线。经计算得BPNN、GS-RF、GA-RF和PSO-RF模型的腐蚀速率预测值与实际值的决定系数R2分别为0.83、0.87、0.92和0.97。其中,PSO-RF模型的R2最接近1,因此其预测效果最优。
随机森林模型作为数据驱动的集成类模型,比一般的浅层模型层数更多,在预测过程中能够综合考虑多个环境因素对腐蚀速率的影响,对于复杂结构的腐蚀数据集预测有较好的适用性;而粒子群优化算法不仅具有全局寻优能力,还拥有高效的信息共享机制。因此集成粒子群优化算法和随机森林算法建立的PSO-RF模型泛化能力最强,预测性能最优,这一模型的建立可为塔河油田集输管道的智能腐蚀风险管理提供思路和方法,以实现更好的安全管理,从而避免潜在事故。
5. 结论
(1)通过Pearson相关性分析和灰色关联度分析,得到塔河油田集输管道内腐蚀的4个主控因素:CO2分压、温度、Cl-含量和H2S分压,以此作为模型输入特征使得模型预测精度大幅提升。
(2)采用PSO算法对RF的超参数进行优化,通过实例研究,证明该方法可有效避免模型寻优过程中陷入局部极值的问题,快速获得全局最优解,并大幅提升预测精度。在寻优次数相同的情况下,PSO的收敛速度比GA快,且PSO的寻优次数仅需2 000次,远低于网格搜索的寻优次数。
(3)针对塔河油田管道复杂的腐蚀数据,PSO-RF模型的整体预测误差较小,σRMSE和σMAE分别为0.161和0.027,R2等于0.97,与BPNN、GS-RF和GA-RF模型相比,该模型预测精度最高,在预测油气管道腐蚀速率方面具有良好的性能。
文章来源——材料与测试网







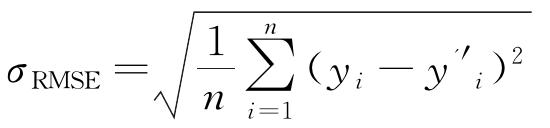







 浙公网安备 33042402000106号
浙公网安备 33042402000106号

