分享：不锈钢薄板平面应力断裂韧度测试

随着经济的发展，不锈钢的应用越来越广泛。目前，针对不锈钢的疲劳开裂及断裂原因分析的研究较多[1-5]，针对除不锈钢外其他材料薄板的断裂韧度也进行了许多研究[6-7]，但对不锈钢薄板平面应力断裂韧度测试的研究较少。不锈钢板平面应力断裂韧度用于描述薄板材料抵抗裂纹扩展的能力，材料断裂韧性试验能够为结构提供抗裂纹扩展特性，并为剩余强度分析提供判据，以保证结构在可检裂纹尺寸范围内不会出现破坏现象。因此，需要对不锈钢材料的平面应力断裂韧性及平面应力状态下抗裂纹扩展的阻力进行研究，以预防结构突然断裂。 

笔者结合标准ASTM E561-22 Standard Test Method for KRCurve Determination，对不锈钢薄板平面应力断裂韧度KC测试的原理进行研究，分析讨论了获取断裂韧度KC的不同方法，并对这些方法进行比较，研究结果可为结构材料的安全提供重要的数据支撑。 

1.   试验原理及试样制备

1.1   试验原理

用应力强度因子表达的材料断裂韧度KR随有效裂纹扩展量Δae变化的曲线称为KR曲线，KR曲线的测试通常采用带有疲劳裂纹的紧凑拉伸C（T）试样，按规定的加载速率对试样进行加载，记录加载过程中的P（载荷）-v（位移）曲线。加载过程中Δae可通过光学法或柔度法获得，而应力强度因子KR可根据相应的表达式计算得出。对有效的（KR，Δae）数据对进行处理即可获得材料的KR曲线。最大载荷点处的数据满足有效性判据，则该点的KR取值即为材料的KC取值。 

1.2   试样制备

试验采用小宽度紧凑拉伸试样C(T)，试样长度为62.5 mm，宽度为50 mm，厚度为1.5 mm，加载孔直径为12.5 mm。 

在疲劳试验机上预制裂纹，过程采用降K法，应力比为0.1，加载频率为5 Hz，波形为正弦波，循环1.9万周次，预制疲劳裂纹长度不小于2 mm。 

2.   试验过程

2.1   断裂试验

以0.5 mm/min的加载速率进行加载，直至裂纹扩展，试样断裂，记录P-v曲线数据。 

2.2   初始裂纹长度测量

试样拉断后，在试样断口上用光学显微镜测量裂纹的初始长度，在试样中央平面及两个1/4平面分别进行测量，将平均值作为预制裂纹标记处的初始裂纹尺寸a0，测量的初始裂纹长度为20.18 mm。 

2.3   有效弹性模量Eeff的测量

由初始裂纹尺寸a0、初始弹性斜率（Δv/ΔP）0，以及柔度校准方程确定有效弹性模量Eeff。对于C(T)试样，使用式（1）的柔度表达式计算Eeff，Eeff与a0的差值应小于试样宽度的0.001倍。 

式中：Δv为位移变化量；ΔP为载荷变化量；E为材料弹性模量；B为试样的厚度；EBΔv/ΔP为试样柔度；a0为初始裂纹长度；W为试样宽度。 

计算得到Eeff=191.24 GPa，材料的弹性模量为200 GPa，检查得到Eeff在弹性模量的10%范围内。有效弹性模量Eeff与初始裂纹尺寸a0相差0.02 mm，符合要求。 

2.4   等效裂纹尺寸的测量

通过割线柔度直接测量有效裂纹尺寸，随后计算需要的物理裂纹尺寸ap，以确定其有效性。根据割线柔度方法，在初始线性区外，沿力-CMOD（裂纹尖端张开位移）曲线选择至少20个数据点。对于每一个分析点（vi，Pi），用式（2），从CMOD原点v0到每一个选择点计算割线的斜率。 

式中：v0为原始点的裂纹张开位移；vi为第i点的裂纹张开位移；Pi为加载力。 

根据割线斜率、试样几何形状及有效弹性模量，用式（3）、（4）柔度表达式，在每一个选择分析点计算有效裂纹尺寸ae。因此，将（vi，Pi）数据点转换成（aei，Pi）。 

式中：U为标准化量。 

2.5   物理裂纹尺寸测量

对于割线柔度方法，物理裂纹尺寸必须由迭代需要的塑性区修正量rY确定。首先将KR代入式（5）的K中，可得到rY的上限值。利用式（6）估计物理裂纹尺寸ap，并计算K（ap），随后将K（ap）代入式（5）的K中，确定rY的下限值。通过反复调整rY，直到将K（ap）代入式（5）时获得相同的rY，从而确定物理裂纹尺寸ap。 

式中：σYS为材料的屈服强度；K为应力强度因子。

3.   试验结果

3.1   扫描电镜（SEM）分析

预制裂纹阶段断口的SEM形貌如图1所示。由图1可知：预制裂纹区域断口较平整，存在解理刻面和解理平面，且有很多台阶，断口上未见韧窝形貌。 

图  1  预制裂纹阶段断口的SEM形貌

裂纹扩展阶段断口的SEM形貌如图2所示。由图2可知：裂纹扩展区域断口不平整，且扩展区域随着载荷的循环加载，逐渐形成三角形；裂纹扩展区呈高韧性形貌，存在大量韧窝，韧窝深度较深，扩展区韧性较好。 

图  2  裂纹扩展阶段断口的SEM形貌

3.2   KR裂纹扩展阻力曲线的测定

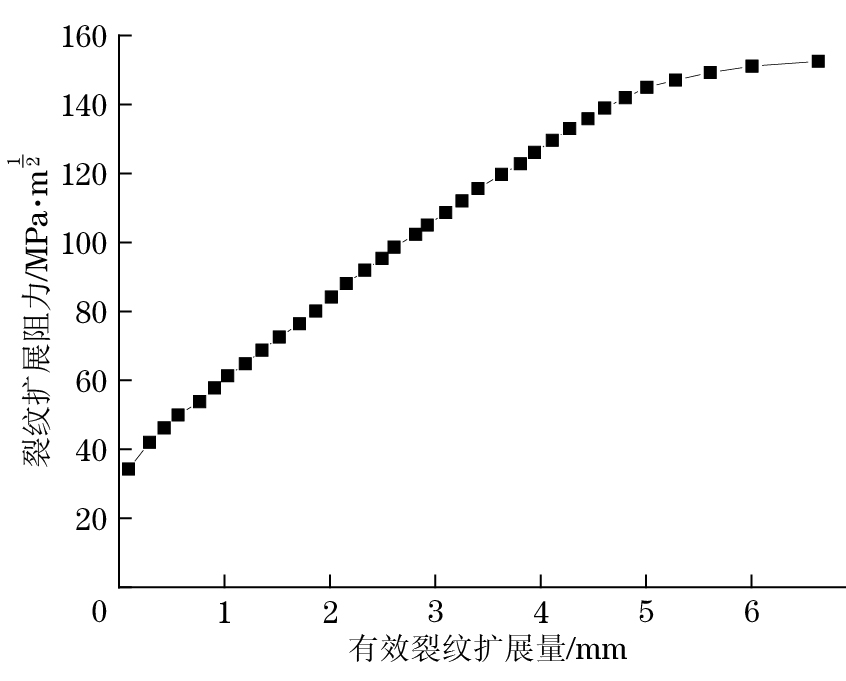
通过割线柔度直接测量有效裂纹尺寸，根据式（7）计算得到有效裂纹扩展量Δae。由KR与Δae原始数据对，结合净截面应力有效性标准ASTM E561-22，测定物理裂纹尺寸及塑性区修正量。根据有效性判定要求，用式（8）计算有效性比值Rv，选取Rv≤1.0对应的KR和Δae有效数据对，绘制裂纹扩展阻力曲线，结果如图3所示。 

3.3   平面应力断裂韧度KC的测定

3.3.1   方法1

根据ASTM E561-22标准，KC是试验中最大力值点对应的KR，即为裂纹尖端应力非平面应变条件下的裂纹扩展阻力。因此，根据原始数据采集力P，且拾取Pmax（最大值），相应的临界有效裂纹尺寸aec为25.38 mm，通过计算得到KC为147 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$。 

KC不仅与材料有关，还取决于试样类型、尺寸和厚度，同时，KC是R曲线和形状相关作用K曲线之间相切处的KR，根据ASTM E561-22 标准，结合试样的裂纹驱动力曲线，确定其与KR曲线相切时所对应的应力强度因子K，即为试样的平面应力断裂韧度KC。 

裂纹驱动力曲线与KR曲线如图4所示。由图4可知：在初始裂纹长度a0至临界裂纹长度ac之间，不同载荷条件下的裂纹扩展驱动力曲线与KR曲线仅有一个交点，载荷随着等效裂纹尺寸的增加而呈单调递增趋势，且在最大载荷Pmax条件下，裂纹扩展驱动力曲线与KR曲线相切，切点为平面应力断裂韧度KC。 

图  4  裂纹驱动力曲线与KR曲线

因此，建立驱动力载荷P与有效裂纹尺寸ae的关系模型，求出在一定有效裂纹长度范围内的最大载荷，从而确定平面应力断裂韧度KC。在选取有效数值区间段，P关于ae具有最大值。即P对ae的一阶导数为0，P对ae的二阶导数小于0。 

下面建立P-ae之间的数值关系，利用最小二乘法拟合，通过拟合回归方程的回归判定系数R2，获取拟合参数。模型选择多项式，多项式随着次数增多，回归判定系数R2越接近于1，拟合效果越好，残差方r2越小，拟合越好。下面对比讨论两种多项式拟合结果，一种是一元三次多项式，另一种是一元四次多项式，通过比较回归判定系数R2及残差方r2，在数据不失真的情况下，找到最佳的P-ae关系模型。 

3.3.2   方法2

建立P-ae一元四次多项式模型，利用最小二乘法拟合多项式，P=B0+B1ae+B2a2e+B3a3e+B4a4e，R2=0.999 53，r2=0.367 74。选取有效数值区间段ae∈[20.5 mm，27.0 mm]，得到拟合参数B0=－837.933 537，B1=142.931 252，B2=－9.246 009 615，B3=0.269 033 199，B4=－0.002 957 675 24；利用函数逼近法，求解得到当aec为25.57 mm时，选取有效数值区间段ae∈[20.5 mm，27.0 mm]，取Pmax最大值，Pmax=4.90 kN，KC=149 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$（见图5）。 

图  5  一元四次多项式模型拟合P-ae曲线

3.3.3   方法3

建立P-ae一元三次多项式模型，利用最小二乘法拟合多项式，P=B0+B1ae+B2a2e+B3a3e，选取有效数值区间段ae∈[20.5 mm，27.0 mm]，得到拟合参数B0=－2.224 58，B1=－2.705 85，B2=0.243 07，B3=－0.004 94，R2=0.998 81，r2=0.977 73，求解得到当aec=25.70 mm时，选取有效数值区间段ae∈[20.5 mm，27.0 mm]，取Pmax最大值，Pmax=4.926 kN，KC=151 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$（见图6）。 

图  6  一元三次多项式模型拟合P-ae曲线

3.4   小结

结合上述结果，比较构建的一元三次和一元四次多项式模型，发现一元四次多项式模型的R2更接近1，r2更小，说明构建的一元四次多项式模型拟合效果更佳。比较利用最大力值点获取平面应力断裂韧度的方法1与构建一元四次多项式模型的方法2，数值偏差为1.36%。比较利用最大力值点获取平面应力断裂韧度的方法1与构建一元三次多项式模型的方法3，数值偏差为2.72%，均相对较小。因此认为3种方法均可采用。 

4.   结论

（1）通过测定不锈钢薄板试样的KR曲线和KC值，获得了稳态裂纹扩展数据，为不锈钢板的实际应用工况提供了基础数据支撑。 

（2）提出了获取Pmax的3种方法，对平面应力断裂韧度进行对比，方法1通过原始数据直接获取最大力Pmax，代入获得KC为147 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$；方法2通过拟合一元四次多项式，在有效裂纹长度范围内求解得到KC为149 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$；方法3通过拟合一元三次多项式，求解得到KC为151 MPa·${\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">?</span>}}^{\frac{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">1</span>}}{\mathrm{<span\; style="font-size:\; 16px;\; color:\; rgb(0,\; 0,\; 0);">2</span>}}}$。其中方法2采用的一元四次多项式拟合效果更佳，与方法1相比数值偏差1.35%，方法3与方法1的数值偏差为2.72%，均相对较小。因此3种方法均可采用。 

（3）建议标准修订能够给出KC测定的具体步骤，以便保证不同检测机构测试结果的一致性。

文章来源——材料与测试网